Determine if tree is AVL in O(n)
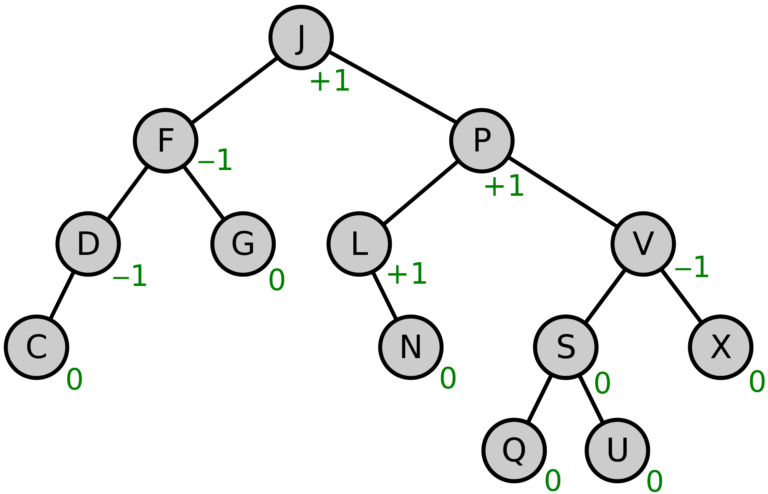
The following java method will determine if a binary tree is AVL (and, obviously BST) /** * This recursive method will calculate if a tree is AVL by returning * its max depth. * * @param t * @param p…
Category Algorithms
Determine max and min root leaf path in a Binary Search Tree (BST)
Let’s view an algorithm that manage to find the minimum and the maximum root-leaf path in a binary search tree. I used three stacks in this algorithm, one is temporary and the other will be filled with the results. Note…
Algorithms on Graphs
Depth-First-Search (DFS) The first kind of visit in a graph is the DFS and its output is: Generate a spanning forest; Visit every edge and every vertex; Determine if the graph is connected; Calculate the connected components of the graph.…
Quickselect algorithm
18 8 3 2 1 5 4 9 10 Suppose we want to know the k-th element of the array, how we would do? We would sort the array, with O(nlogn) for example Then we will get the element searched But…